What makes for a good inference?

What is inference and why does it matter?

Data Proliferation [source]

We live in a sea of data and information, but rarely does information
translate to  insight! What the  domain experts look for the most is the
ability to make better decisions based upon insights (beer and diaper
story comes to mind -- although it is an urban legend). A better
example is the economist experiment:

• Offer A: online Subscription for $60,
• Offer B: Print only subscription for $120
• Offer C: Print and online subscription for $120

The insight here was that people will switch to print+online offer as
it is perceived to be the best offer. The key is in providing a set of
choices that results into the desired outcome.

In analytics, we try hard to find such insights and help influence
business decisions. However, very frequently the decisions taken are
very mundane -- Should the large size of the cereal box be 20oz or 21oz?


What are commonly used inference methods?

So, how do analysts go from data to insights?
If you come from statistics background, you would fall back on the concept of
hypothesis testing. You propose a hypothesis, try to find the odds
that the hypothesis holds (frequently the null hypothesis being
rejected). The idea is simple but elegant. Suppose you observe a
person who is 99 years old and then try to answer the question: what
is the expected life span? Clearly you can't say its 99 years as you
don't know if that is an outlier or the norm.

What are some of the drawbacks of statistical inference methods?

Hypothesis makes this approach precise -- it can tell you how the odds
change as a function of the number and type of your
observations. However, a lot of us frequently forget about the
assumptions that go into hypothesis testing and as a result the
conclusions may not be reliable (Does your data really have normal
error distribution? Is your data really independent/uncorrelated as
required -- for example if your data is some type of timeseries it
probably has a fair degree of autocorrelation).


I have an interesting anecdote for this. We were testing a set of
models which had a couple of hundred coefficients. We found that about
5% were flagged as non-zero with a p-value of 5%. If you were to
blindly accept all the significant outcomes based on the p-values you
would lose the big picture. 5% p-value says that you can expect 5%
type-2 errors (reject the null hypothesis incorrectly) and that is
what we found in the data. But, wait that is not sufficient. We also
checked the values and found them to be close to zero (0.1, 0.05 etc)
and hence it made sense to conclude that the current formulation
wasn't finding any significant coefficients.

Below is another example for using a t-test on two populations. This is usually used for determining if there are significant differences between two datasets. This could have many different applications -- clinical trials for testing the efficacy of a drug, A/B testing of offers both in the online and offline worlds etc.

The simulation below demonstrates that it is possible to conclude incorrectly if the results are based on a single statistical measure (the p-value). Confidence interval provides yet another measure that has the nice property of convergence as the sample size increases.

First example is on a simulation of randomly generated uniform [0,1] (or U(0,1) random variables. The second example uses standard normal (N(0,1)) random variable with mean = 0 and variance = 1.

CI and p-values for simulated data

We generate two samples from the same population (uniform [0,1] i.i.d
random variables) and then run a t-test with the null hypothesis that
the means are equal. A low p-value (<10% or 5%) would cause us to
reject the null hypothesis and conclude that the means are likely
different.

As you can see, even as the sample size increases the p-value tends to
bounce around (including some cases where it dips below 10% threshold
-- not shown here). On the other hand the confidence interval does a
much better job at concluding that they are identical. Notice how
quickly the spread narrows.

Now the same experiment run on N(0,1). I have added points for the sample means, which are indeed close to 0 (the expected value).

If we pick a p value threshold of 10%, we will reject the null
hypothesis in some of the cases. Apart from the chance occurrence,
when you have large sample sizes, the variances could be small enough
to give you this result.

So, how do I know this is indeed the case? I used random number
generator to generate two sets with the _same_ parameters (uniform
random numbers U[0,1] in the first example and N(0,1) random numbers in the second)

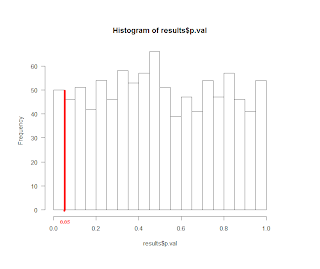
Next, I ran a simulation where I generated two independent vectors of 1000 N(0,1) variables and computed the p-value and confidence intervals. The figure shows that the confidence interval and sample mean (yellow) estimate is indeed clustered around 0, but the p-value (green) is bouncing around quite a bit. Subsequent figure shows the histogram of the p-values from the same experiment. As expected, we find that 5% of the p-values are less than 0.05!

How can you improve inference techniques?

What we need is higher degree of confidence in our
inferences. However, since we are reducing a large amount of data to a
few outcomes, it becomes necessary to look at multiple things. As one
gains experience, it is easy to refine the key metrics and focus on
the right subset.

1. Most statistical packages (R, SAS) report a number of useful
statistics when estimating a model -- please understand what each of
them mean and look at them carefully. Look at the p-values,
t-statistics, AIC/BIC values, deviance values, reduction from null
deviance, degrees of freedom etc

2. The model estimation is influenced by data and in some cases more
so by some data points than others. Once you understand this, looking
for outliers and leverage (shows relative contribution of the data
points to the coefficient estimates) becomes the norm.

3. Confidence bands/intervals: This gives you a much better feel for
the possible range of values that the outcome can take. For example,
in an election if one of the candidate is leading by 55% vs 45% and
the margin of error (difference between the midpoint and one of the
ends of the confidence interval) is 6%, then the results could reverse
the direction during the final outcome.


4. Withhold some data from your training set and run the estimated
models on this withheld set to see how well it can fit that data --
this is one of the most important test you can run to ensure the
validity of your model. There are many creative ways of doing this:
cross-validations, leave-one-out method, pick specific data-points for
withholding etc.

5. Bring in the problem context at hand to see what are the important
problem related metrics that one can use. In the retail sector, the
most important metric one can use is the forecast accuracy for the
demand or the sales. In the clinical trial area it could be a
measurement of related outcomes -- longevity, survival time etc.

6. Find out the basic approaches advocated by the academic or
industry practitioners (and Google search is your friend!) -- see what
works for others and what doesn't. If nothing else, it will expedite
your model development and validation process.

7. Train models on simulated data. This is a great way to ensure that
there are no coding/interpretations issues. You should be able to
simulate fairly complex data and should be able to recover all the
driving parameters that went into the model. In fact, this can serve
as a very good automated test suite to validate model enhancements.